真偽表を使うことで複雑な論理関係を明快に理解することができます.
いくつかの命題が与えられたとき,それらを論理演算子で組み合わせて新しい命題をつくることができます.代表的な論理演算子としては,否定(でない),論理和(または),論理積(かつ),含意(ならば),同値 などがあります.
与えられた命題の真偽の組み合わせによって,新しくつくった命題の真偽が決まります.この対応を明確に見るための道具が真偽表 (真理表,真理値表)と呼ばれるものです.真偽表は学校ではおそらく習わないので多くの人は知らないと思いますが,考えている命題が複雑になるほど威力を発揮するとても便利な道具なので,知っておいて損はないでしょう.
命題 $P$ について,『$P$ でない』という命題を $P$ の否定といい,$\bar{P}$ (または $\lnot P$) で表します. $P$ がどのような命題であっても,$P$ の真偽と $\bar{P}$ の真偽は必ず逆転します.つまり,$P$ が真ならば $\bar{P}$ は偽となり,$P$ が偽ならば $\bar{P}$ は真となります.この関係を真偽表で書くと以下のようになります.
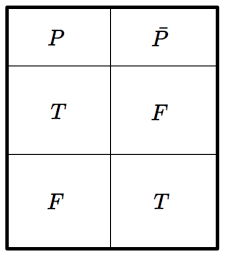
$T$ は真,$F$ は偽を表しています.真偽表の一番左の列は,$P$ のとりうる真偽値が書かれています.各行について右に進むと,$P$ が真のときは $\bar{P}$ が偽で,$P$ が偽のときは $\bar{P}$ が真であることがわかります.
$2$ つの命題 $P,Q$ について,『$P$ または $Q$』という命題を $P\lor Q$ で表します.$P\lor Q$ は $P$ と $Q$ の少なくとも一方が真であるときに限り真となります.
また,『$P$ かつ $Q$』という命題を $P\land Q$ で表します.$P\land Q$ は $P$ と $Q$ がともに真であるときに限り真となります.$P\lor Q$ と $P\land Q$ の真偽表は次のようになります.
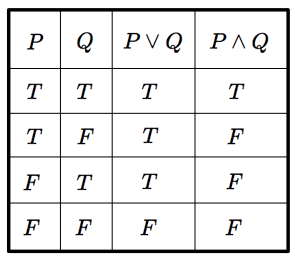 まず,左の $2$ 列について,$P,Q$ の真偽値のとりうる組み合わせは $2^2=4$ 通りあるので,それらの組み合わせがすべて真偽表にあらわれています.(したがって,真偽表は $4$ 行になります) 各組み合わせについて,その行を右に進んで見れば,$P\lor Q$ と $P\land Q$ の真偽がわかります.
まず,左の $2$ 列について,$P,Q$ の真偽値のとりうる組み合わせは $2^2=4$ 通りあるので,それらの組み合わせがすべて真偽表にあらわれています.(したがって,真偽表は $4$ 行になります) 各組み合わせについて,その行を右に進んで見れば,$P\lor Q$ と $P\land Q$ の真偽がわかります.
たとえば,$P$ が真で,$Q$ が偽のときは,$2$ 行目を右に進んで見れば,$P\lor Q$ は真で,$P\land Q$ は偽であることがわかります.
$2$ つの命題 $P,Q$ について,『$P$ ならば $Q$』という命題を $P \Rightarrow Q$ (または $P\rightarrow Q$) で表します. $P\Rightarrow Q$ は,$P$ が真で $Q$ が偽のときに限り偽となります.
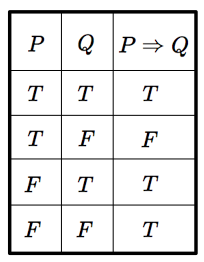
$P$ ならば $Q$ について, $P$ にあたる命題を前提といい,$Q$ にあたる命題を結論といいます.前提 $P$ が偽のときは $P\Rightarrow Q$ は常に真であることに注意してください. (注) $P\Rightarrow Q$ は,$Q\Leftarrow P$ と書いても同じことです.ただし,当然,$P\Rightarrow Q$ と $P\Leftarrow Q$ は別の命題です.
さて,ここまでで,否定,かつ,または,含意 の真理値がどうなるかを紹介してきました.実は,どんなに複雑な命題もいくつかの命題と,これら $4$ つの論理演算子の組合せで表すことができます.したがって,これら $4$ つの真理値の規則だけ覚えておけば,真偽表を使って,どんな状況にも対応できます.つぎの同値がいい例です.
(注) 実は,かつ と 含意 はともに 否定 と または の組合せで表すことができる (練習問題参照)ので,実質, 否定と または だけで表現できるのですが,かつ と 含意 も基本的な論理演算子なので覚えたほうがよいです.
同値
『($P$ ならば $Q$)かつ($Q$ ならば $P$)』,すなわち『($P\Rightarrow Q$)$\land$($Q \Rightarrow P$)』という命題を $P \Leftrightarrow Q$ で表します. $P \Leftrightarrow Q$ の真偽値がどうなるのか,真偽表を用いて確認してみましょう. まず,$P$ と $Q$ のとりうるすべての組み合わせ ($4$ 通り) を下のように書きます.
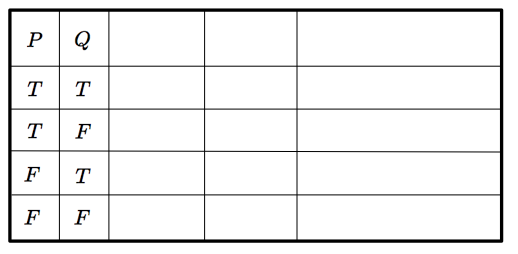
つぎに,いきなり ($P\Rightarrow Q$)$\land$($Q \Rightarrow P$) の真偽値を求めるのはややこしいので, $P\Rightarrow Q$ と $Q \Rightarrow P$ と ($P\Rightarrow Q$)$\land$($Q \Rightarrow P$) の $3$ つを表の一番上の行に書きます.最終的に知りたいのは一番右の列がどうなるかです.

含意とかつの推論規則を使って,各行について,右に進んで真偽を埋めていきます.
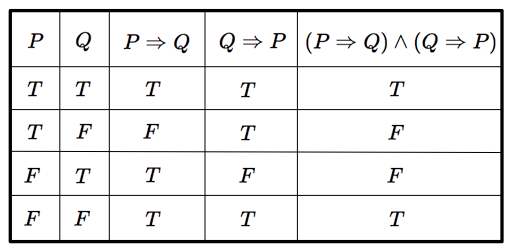 したがって,$P\Leftrightarrow Q$ の真偽はつぎのようになります.
したがって,$P\Leftrightarrow Q$ の真偽はつぎのようになります.
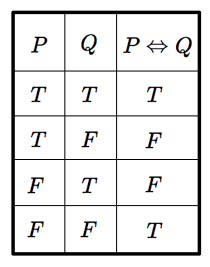
つまり,$P\Leftrightarrow Q$ は,$P$ と $Q$ の真偽が一致しているときに限り真となります. このように,複雑な論理式で表された命題も,真偽表を使って順番に考えていけば,その真偽がどのようになっているか求めることができます.
真偽表の有用性を練習問題を通して確かめましょう.
問 $\bar{P}\lor Q$ と $P\Rightarrow Q$ の真偽値がつねに一致することを確かめよ.つまり,命題 $P,Q$ の真偽によらず,命題 ($\bar{P}\lor Q$)$\Leftrightarrow$($P\Rightarrow Q$) は真である.
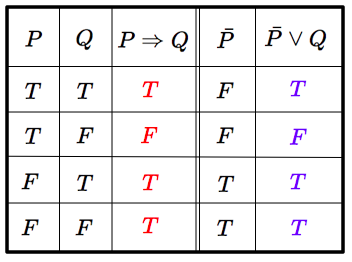
問 命題に関するド・モルガンの法則を真偽表を用いて確かめよ.つまり,以下の $2$ つの命題が,命題 $P,Q$ の真偽によらず,常に真であることを示せ.
$$ \overline{P \lor Q} \Leftrightarrow \bar{P} \land \bar{Q}$$ $$ \overline{P \land Q} \Leftrightarrow \bar{P} \lor \bar{Q}$$
一つ目の式のみ示す.
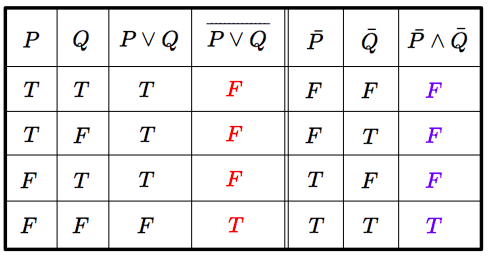
二つ目の式も同様に真偽表をつくれば確かめることができる.
問 対偶証明法の正当性を真偽表を用いて確かめよ.
命題 $P,Q$ の真偽によらず,$P \Rightarrow Q$ の真偽値と $\bar{Q} \Rightarrow \bar{P}$ の真偽値がつねに一致することを示せばよい.
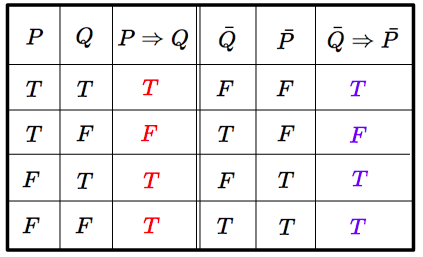
つまり,命題 $(P \Rightarrow Q) \Leftrightarrow (\bar{Q} \Rightarrow \bar{P})$ は真である.(これは対偶証明法の正当性を示している)
問 (背理法の正当性)
$P,Q,R$ を命題とする.『$P \Rightarrow Q$』 の真偽値と 『$(P \land \bar{Q}) \Rightarrow (R\land \bar{R})$』の真偽値がつねに一致することを真偽表を用いて確かめよ.
$P\Rightarrow Q$ を背理法で証明することの正当性を確かめる問題. $P,Q,R$ の真偽のとりうる組み合わせは $2^3=8$ 通りあるが,$8$ 行の真偽表を書く必要はない.なぜなら,$R\land \bar{R}$ はつねに偽であるから,$R$ が真か偽かを考慮しなくてよい.
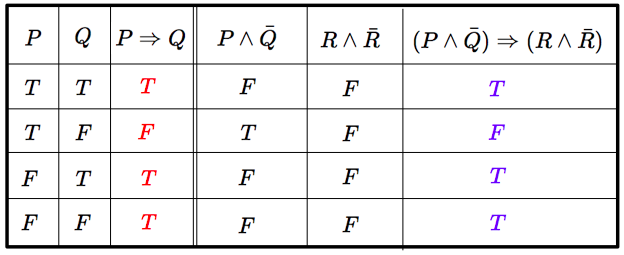
よって,命題 $(P \Rightarrow Q)\Leftrightarrow ((P \land \bar{Q}) \Rightarrow (R\land \bar{R}))$ は真である.