ガウス記号の基礎事項について解説します.まず,整数部分,小数部分とは次のようなものです.
整数部分: 実数 $x$ に対して,$x$ を超えない最大の整数がただひとつ存在し,それを $[x]$ と書き,$x$ の整数部分と呼ぶ.
小数部分: 実数 $x$ に対して,$x-[x]$ を $x$ の小数部分と呼ぶ.
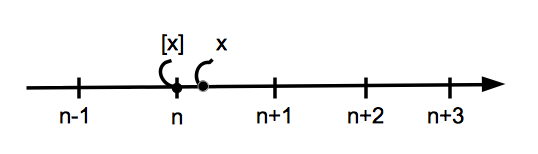
このときの記号 $[ ]$ をガウス記号と呼びます.つまり,ガウス記号は実数の整数部分を表すための記号です. さて,いかなる実数 $x$ に対しても,$n \le x < n+1$ となる整数 $n$ がただひとつ存在します.わかりにくければ,数直線を思い描いてみてください.数直線を整数点ごとに区切っていきます.すると,数直線は幅 $1$ の区間に分割されます.実数 $x$ はこれらの区間のいずれかに入っています.そこで,$x$ が入っている区間の左端の整数点を $[x]$ と表記するということです.
たとえば, $$[3]=3,\ \ \left[\frac{1}{2}\right]=0,\ \ [-4.3]=-5,\ \ [\pi]=3,\ \ \left[-\sqrt{5}\right]=-3$$ などが成り立ちます.実数 $x$ が負のときは少し注意が必要です.たとえば,$-4.3$ の整数部分は $-4$ ではなく,$-5$ です.また,$-4.3$ の小数部分は $0.3$ ではなく,$0.7$ です.整数部分は,数直線を頭で思い描けば間違えることはないでしょう.小数部分は,$x-[x]$ という定義通り計算すれば間違えません.言葉に惑わされないようにしましょう.
ガウス記号を用いたグラフについて考えてみましょう. $$y=[x]$$ という関数のグラフはどのようになるでしょうか.これはさきほどと同様に数直線で考えてみればわかります.$0 \le x 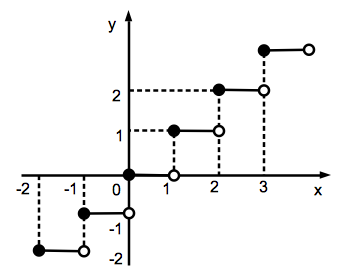
ただし,上のグラフについて,黒丸は端点を含み,白丸は端点を含まないことを示しています.$y=[x]$ のグラフはこのような階段状になっています.このグラフの最大の特徴は連続でないということです.高校までの数学で習う多くの関数 (一次関数,二次関数,三角関数,指数関数,無理関数など) はすべて連続な関数です.つまり,値が急に“ジャンプ”するようなことはありません.ところが,$y=[x]$ は $x$ が整数値をとるところで値が“ジャンプ”しています.すなわち,すべての整数点で不連続な関数となっています.
ガウス記号に関して,以下の基本的な事柄が成り立つことは覚えておきましょう.
$x,y$ を実数,$n$ を整数とする.以下が成り立つ. ・$[x]=n$ ⇔ $n \le x < n+1$ ⇔ $x-1 < n \le x$ ・$[x+y] \ge [x]+[y]$
・$[x+n]=[x]+n$
一番目はガウス記号の定義からほとんど明らかです.$n \le x < n+1$ ⇔ $x-1 < n \le x$ は意外とよく使います.$n$ と $x$ のどちらを基準にして不等式ではさむかということだけです . 二番目の不等式の意味合いは次のようになります.
($2$ つの実数を足してから,小数部分を切り捨てたもの) $\ge$ ($2$ つの実数の小数部分をそれぞれ切り捨ててから足したもの)
このように言葉で理解したほうが覚えやすいかもしれません. 左辺は,ガウス記号の中身の足し算をしたときに,繰り上がる可能性があります.たとえば,$x=2.4, y=3.7$ とすると, $$[x+y]=[6.1]=6, [x]+[y]=2+3=5$$ 繰り上がった場合は左辺の方が大きくなります.
ガウス記号が絡むと問題が急に難しくなったように感じます.